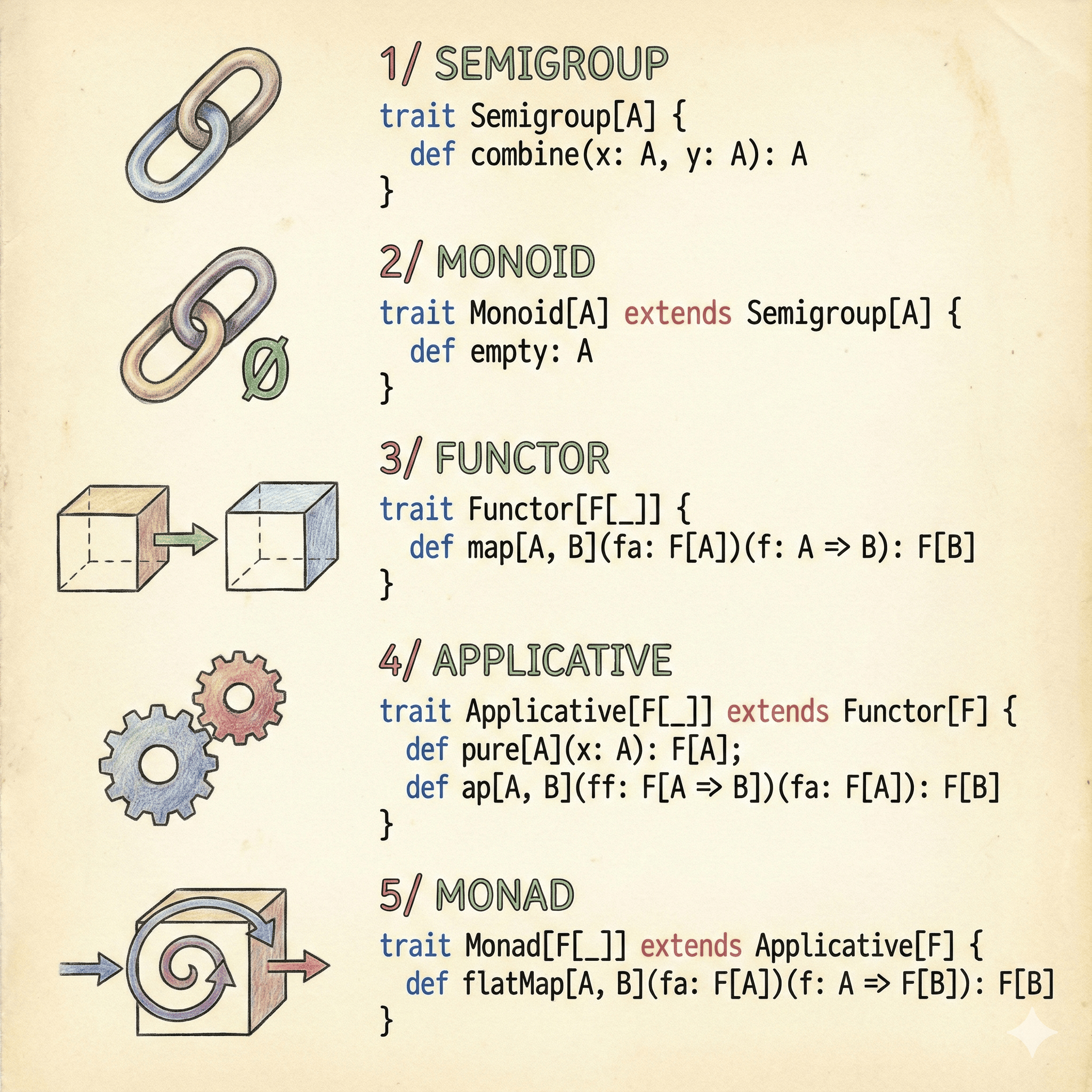
Functional Programming Abstractions in Scala

Master the foundation of modern Scala development by exploring five essential functional programming abstractions. This guide takes a deep dive into algebraic structures, starting with Semigroup and Monoid for combining values. It progresses to type constructors, explaining how Functors transform wrapped data, Applicatives combine independent contexts, and Monads sequence dependent computations. By understanding these core patterns, developers can write more polymorphic, composable, and algebraically sound Scala code that works across diverse data types.

Introduction
Semigroup
- Intuition
- Associativity Law
Monoid
Functor
- Overview
- Lifting function examples
Applicative
Monad
- Overview
  - Monadic Combinators
  - Monadic Types
- Scala Implementation
References

Introduction

These five abstractions form the foundation of functional programming. They represent purely algebraic structures defined only by their operations and the laws governing them. Understanding these concepts allows you to:

Recognize patterns across different problem domains
Write polymorphic code that works with many data types
Reason algebraically about program behavior
Compose operations to build complex functionality from simple pieces

These abstractions are discovered, not invented. They emerge naturally from observing common patterns in our code.¹

I am going to discuss the following:

Functional Abstractions

Semigroup

A Semigroup is the simplest algebraic structure: a type with an associative binary operation. It captures the essence of “combining” things together, where the order of grouping doesn’t matter.²

Intuition

Think about combining elements in everyday life:

String concatenation: "Hello" + " " + "World"
Adding numbers: 1 + 2 + 3
Merging lists: List(1,2) ++ List(3,4) ++ List(5,6)

In all these cases, you can group operations in any order:

(a + b) + c produces the same result as a + (b + c)

This property is called associativity, and it’s what makes a Semigroup useful for parallel computation.³

---
config:
  look: neo
  theme: default
---
graph LR
    A[Element a] -->|combine| D[Result]
    B[Element b] -->|combine| D
    C[Element c] -->|combine| D
    
    style D fill:#4CAF50
    style A fill:#2196F3
    style B fill:#2196F3
    style C fill:#2196F3

Diagram Explanation: Elements combine using the binary operation, and the grouping order doesn’t affect the final result.

Formal Definition: A semigroup consists of:

A set $S$ (in Scala, this is a type A)
A binary operation $\bullet: S \times S \to S$ (written as combine in Scala)

Type Class Definition⁴:

trait Semigroup[A] {
    // Associative binary operation
    def combine(first:A, second:A): A
}

defined trait Semigroup

Example📝⁴ for Semigroup for String concatenation:

// The implicit val declaration makes this Semigroup instance automatically available 
// whenever a Semigroup[String] is needed, without explicitly importing/passing it
// It allows String concatenation to work with Semigroup operations automatically
// The compiler will use this implicit value to resolve Semigroup[String] requirements

implicit val stringSemigroup: Semigroup[String] = new Semigroup[String] {
    def combine(first: String, second:String): String = first + second
}

stringSemigroup: Semigroup[String] = ammonite.$sess.cmd1$Helper$$anon$1@3d09f387

// Example using stringSemigroup to combine two strings
val result = stringSemigroup.combine("Hello", " world!")

result: String = "Hello world!"

Example📝⁴ for Semigroup for integer addition:

implicit val initSemigroup: Semigroup[Int] = new Semigroup[Int] {
    def combine(first: Int, second: Int): Int = first + second
}

initSemigroup: Semigroup[Int] = ammonite.$sess.cmd3$Helper$$anon$1@4d35f028

initSemigroup.combine(1,2)

res4: Int = 3

Associativity Law

For all elements $a, b, c \in S$:

\[(a \bullet b) \bullet c = a \bullet (b \bullet c)\]

Translation: $\bullet$ means “combine”. The equation says that combining $a$ and $b$ first, then combining the result with $c$, gives the same answer as combining $a$ with the result of combining $b$ and $c$.

def verifyAssociativity[A] (a: A, b: A, c: A)(implicit sg: Semigroup[A]): Boolean = {
    val leftGrouped = sg.combine(sg.combine(a ,b) ,c)
    val rightGrouped = sg.combine(a, sg.combine(b ,c))
    leftGrouped == rightGrouped                              
}

defined function verifyAssociativity

The implicit parameter sg: Semigroup[A] means that this method requires a Semigroup instance for type A. The implicit keyword allows the compiler to automatically find and pass a Semigroup[A] value that is in scope when this method is called Semigroup is a type class that provides a combine operation for values of type A.

verifyAssociativity(1,2,3)

res6: Boolean = true

Not all operations are associative. Integer subtraction is NOT⁵ a semigroup, for example.

Semigroups don’t require commutativity. String concatenation is associative but NOT commutative.

Monoid

The name monoid comes from mathematics. In category theory, it means a category with one object.

Overview

A Monoid extends Semigroup by adding an identity element (also called “unit” or “zero”). It’s like having a “neutral” value that doesn’t change things when combined.⁶

Intuition

Think of identity elements in everyday operations:

Addition: 0 is the identity → 5 + 0 = 5
Multiplication: 1 is the identity → 5 * 1 = 5
String concatenation: "" (empty string) is the identity → "Hello" + "" = "Hello"
List concatenation: List() is the identity → List(1,2) ++ List() = List(1,2)

The identity element is like a “do nothing” value that acts as a starting point for combining elements.⁷

---
config:
  look: neo
  theme: default
---
graph TD
    A[Monoid] --> B[Semigroup]
    A --> C[Identity Element]
    B --> D[Associative Combine]
    C --> E[Left Identity]
    C --> F[Right Identity]
    
    style A fill:#FF9800
    style B fill:#4CAF50
    style C fill:#2196F3
    style D fill:#9C27B0
    style E fill:#00BCD4
    style F fill:#00BCD4

A Monoid consists of a Semigroup (associative combine operation) plus an identity element that satisfies left and right identity laws.

Formal Definition: A monoid $(M, \bullet, e)$ consists of:

A set $M$ (type A in Scala)
A binary operation $\bullet: M \times M \to M$ (the combine from Semigroup)
An identity element $e \in M$ (called empty in Scala)

Monoid Laws:

1. Associativity (inherited from Semigroup): $(a \bullet b) \bullet c = a \bullet (b \bullet c)$

2. Left Identity: $e \bullet a = a$

Translation: Combining the identity element $e$ with any element $a$ (from the left) returns $a$ unchanged.

3. Right Identity: $a \bullet e = a$

Combining any element $a$ with the identity element $e$ (from the right) returns $a$ unchanged.

Monoid extends Semigroup and adds an identity element

trait Semigroup[A] {
  def combine(first: A, second: A): A
}

trait Monoid[A] extends Semigroup[A] {
    def empty: A // The identity element that leaves other elements unchanged
}

defined trait Semigroup
defined trait Monoid

Example 📝⁸ integer addition Monoid:

implicit val intAddMonoid: Monoid[Int] = new Monoid[Int] {
    def combine(first: Int, second: Int): Int = (first + second)
    def empty: Int = 0
}

intAddMonoid: Monoid[Int] = ammonite.$sess.cmd1$Helper$$anon$1@50c48694

some example Monoid additions:

intAddMonoid.combine(1,0)
intAddMonoid.combine(0,1)
intAddMonoid.combine(1,2)

res9_0: Int = 1
res9_1: Int = 1
res9_2: Int = 3

String Monoid example

implicit val strContactMonoid: Monoid[String] = new Monoid[String] {
    def combine(first: String, second: String) = first + second 
    def empty: String = ""
}

strContactMonoid: Monoid[String] = ammonite.$sess.cmd2$Helper$$anon$1@12fda1b6

String examples are:

strContactMonoid.combine("Hello", " World")
strContactMonoid.combine(strContactMonoid.empty, "Hello")
strContactMonoid.combine("Hello", strContactMonoid.empty)

res11_0: String = "Hello World"
res11_1: String = "Hello"
res11_2: String = "Hello"

List concatenation monoid:

implicit def listMonoid[A]: Monoid[List[A]] = new Monoid[List[A]] {
    def combine(first: List[A], second: List[A]) : List[A] = first ++ second
    def empty: List[A] = List.empty[A]
}

defined function listMonoid

example:

listMonoid.combine(List(1,2), List(3,4))

res13: List[Int] = List(1, 2, 3, 4)

Verify monoid laws:

listMonoid.combine(List(1,2), List.empty[Int]) == List(1,2) // Test left identity
listMonoid.combine(List.empty[Int] ,List(1,2)) == List(1,2) // Test right identity

res14_0: Boolean = true
res14_1: Boolean = true

Test associativity: $(a \bullet b) \bullet c = a \bullet (b \bullet c)$

val a:List[Int] = List[Int](1,2)
listMonoid.combine(listMonoid.combine(a, List.empty[Int]), List.empty[Int]) == 
     listMonoid.combine(List.empty[Int] ,listMonoid.combine(a, List.empty[Int]))

a: List[Int] = List(1, 2)
res15_1: Boolean = true

Use of Monoid

Monoids are perfect for folding/reducing collections because the identity element provides a natural starting point.

Here the fold left/right:

def foldRight[B](z: B)(f: (A, B) => B): B
def foldLeft[B](z: B)(f: (B, A) => B): B

According to associativity and identity laws, the output of the fold left or right should be the same:

def foldLeftWithMonoid[A](elements: List[A])(implicit monoid: Monoid[A]): A = {
  elements.foldLeft(monoid.empty) { (accumulator, currentElement) =>
    monoid.combine(accumulator, currentElement)
  }
}

// Sum a list of integers
foldLeftWithMonoid(List(1, 2, 3, 4, 5))  // Returns: 15

// Concatenate strings
foldLeftWithMonoid(List("Hello", " ", "World"))  // Returns: "Hello World"

// Works with empty lists too!
foldLeftWithMonoid(List.empty[Int])  // Returns: 0 (the identity element)

defined function foldLeftWithMonoid
res3_1: Int = 15
res3_2: String = "Hello World"
res3_3: Int = 0

The output of the above is the same as the following:

def foldRightWithMonoid[A](elements: List[A])(implicit monoid: Monoid[A]): A = {
  elements.foldRight(monoid.empty) { (accumulator, currentElement) =>
    monoid.combine(accumulator, currentElement)
  }
}

// Sum a list of integers
foldRightWithMonoid(List(1, 2, 3, 4, 5))  // Returns: 15

// Concatenate strings
foldRightWithMonoid(List("Hello", " ", "World"))  // Returns: "Hello World"

// Works with empty lists too!
foldRightWithMonoid(List.empty[Int])  // Returns: 0 (the identity element)

defined function foldRightWithMonoid
res17_1: Int = 15
res17_2: String = "Hello World"
res17_3: Int = 0

The Implicit Parameter

Here’s the key part. In foldLeftWithMonoid, the parameter implicit monoid: Monoid[A] means:

“This function accepts a Monoid[A], but I don’t want the caller to pass it explicitly. Scala, look around in scope and find an implicit value of type Monoid[A] for me automatically.”

So when you call foldLeftWithMonoid(List(1, 2, 3, 4, 5)), here’s what happens:

Scala infers the type parameter A is Int (from the list contents)
Scala looks for an implicit Monoid[Int] in scope
It finds intAddMonoid and uses it automatically
The function folds left: 0 + 1 + 2 + 3 + 4 + 5 = 15

With List("Hello", " ", "World"), Scala finds strConcatMonoid (for Monoid[String]) and uses that instead.

Why This Is Elegant

Without implicit, you’d have to call foldLeftWithMonoid(List(1, 2, 3))(intAddMonoid) every time for the Integer list. The implicit mechanism lets the same function work with any type that has a Monoid instance, and the right instance is automatically selected based on the data type. It’s dependency injection built into the language, enabling genuinely polymorphic code while keeping call sites clean.

Parallel Computation with Identity

Split work across multiple threads. Each thread can start with the identity element. For example 📝⁹:

def parallelReduce[A](elements: List[A])(implicit monoid: Monoid[A]): A = {
  if (elements.length <= 1) {
    elements.headOption.getOrElse(monoid.empty)
  } else {
    // balanced fold
    val (leftHalf, rightHalf) = elements.splitAt(elements.length / 2)
    
    // Each half starts from identity and combines
    val leftResult = parallelReduce(leftHalf)
    val rightResult = parallelReduce(rightHalf)
    
    monoid.combine(leftResult, rightResult)
  }
}

defined function parallelReduce

Common Pitfalls

❌ No Valid Identity Element:

Some semigroups cannot be monoids. Example: positive integers with multiplication have an identity (1), but non-empty lists don’t have an identity element.¹⁰

❌ Multiple Possible Identities:

For a given type and operation, there should be only ONE identity element

Integer addition: only 0 is the identity. Integer multiplication: only 1 is the identity. These are DIFFERENT monoids on the same type!

Functor

Overview

A Functor is a type constructor F[_] (like List, Option, Future) that supports a map operation. Functors let you apply a function to values inside a “container” or “context” without manually extracting and wrapping values.¹¹ Example:

trait Foldable[F[_]] {
  def foldRight[A,B](as: F[A])(z: B)(f: (A,B) => B): B
  def foldLeft[A,B](as: F[A])(z: B)(f: (B,A) => B): B
  def foldMap[A,B](as: F[A])(f: A => B)(mb: Monoid[B]): B
  def concatenate[A](as: F[A])(m: Monoid[A]): A =
    foldLeft(as)(m.zero)(m.op)
}

Here we’re abstracting over a type constructor F. We write it as F[_], where the underscore indicates that F is not a type but a type constructor that takes one type argument. Just like functions that take other functions as arguments are called higher-order functions, above Foldable is a higher-order type constructor or a higher-kinded type.

Functors are well explained in my post Scala 2 Functors explained.

Example: The distribute method is automatically provided by composing map with the projection functions (_._1 and _._2), demonstrating a useful property derived from the core map function.

The Functor trait is a type class that defines a basic capability: the ability to apply a function inside a generic container type.

F[_] (Higher-Kinded Type): This means the Functor trait works with any type constructor F that takes a single type parameter. Examples include List, Option, or Future.
map Method: This is the heart of the Functor. It takes a container of type F[A] and a function f: A => B. It applies f to every element inside the container and returns a new container F[B]. This operation lifts the function f into the context F.
distribute Method: This method is derived automatically (a freebie!) from the map method.
- It takes a container of tuples, F[(A, B) (e.g., a List of tuples).
- It uses two map calls: one to extract all the first elements (_._1) into an F[A], and one to extract all the second elements (_._2) into an F[B].
- It effectively splits a container of pairs into a pair of containers: (F[A], F[B]).

// Define the Functor trait as provided in the prompt.
trait Functor[F[_]] {
  def map[A,B](fa: F[A])(f: A => B): F[B]
  
  // The 'distribute' method is automatically derived from 'map'
  def distribute[A,B](fab: F[(A, B)]): (F[A], F[B]) = (map(fab)(_._1), map(fab)(_._2)) // 🤗
}

defined trait Functor

To make the Functor trait useful, we need to create a specific implementation (an “instance”) for a concrete container type, in this case, List.

implicit val listFunctor: Functor[List] = new Functor[List] {
// F is List, so fa is List[A] and the result is List[B]
override def map[A, B](fa: List[A])(f: A => B): List[B] = fa.map(f) 
}

listFunctor: Functor[List] = ammonite.$sess.cmd1$Helper$$anon$1@3db44283

implicit val listFunctor: The use of implicit makes this instance available to the Scala compiler. When the compiler sees a function that requires a Functor[List], it can automatically fetch this value.
Implementation Detail: Since List already has a built-in map method with the exact required signature, the implementation is trivial: we simply delegate to the existing List.map(f). This shows that any type with a compatible map method is a Functor.

The following section shows the standard usage of mapping a transformation over the container.

// We can access the implicit listFunctor instance via its type
val F = listFunctor

// ----------------------------------------------------
// 2. Demonstration of `map`
// ----------------------------------------------------

val sourceList = List(1, 2, 3, 4, 5)
val timesTwo: Int => Int = x => x * 2

// Apply the Functor's map method
val mappedList = F.map(sourceList)(timesTwo)

println(s"Original List: $sourceList")
println(s"Mapping (x => x * 2): $mappedList")
// Expected Output: List(2, 4, 6, 8, 10)

Original List: List(1, 2, 3, 4, 5)
Mapping (x => x * 2): List(2, 4, 6, 8, 10)

F: Functor[List] = ammonite.$sess.cmd1$Helper$$anon$1@3db44283
sourceList: List[Int] = List(1, 2, 3, 4, 5)
timesTwo: Int => Int = ammonite.$sess.cmd2$Helper$$Lambda$2095/0x000000012f7cc208@283b11cc
mappedList: List[Int] = List(2, 4, 6, 8, 10)

Here, the listFunctor (F) takes the sourceList and the timesTwo function, applies the function element-wise, and correctly produces a new list with the doubled values.

Let us see how to use the distribute function: 🤗

// ----------------------------------------------------
// 3. Demonstration of `distribute`
// ----------------------------------------------------

// Create a list of tuples (F[(A, B)])
val pairedData: List[(String, Int)] = List(
  ("Apple", 10),
  ("Banana", 20),
  ("Cherry", 30)
)

// Apply the Functor's distribute method.
// It takes the List[(A, B)] and returns (List[A], List[B])
val (names, counts) = F.distribute(pairedData)

pairedData: List[(String, Int)] = List(
  ("Apple", 10),
  ("Banana", 20),
  ("Cherry", 30)
)
names: List[String] = List("Apple", "Banana", "Cherry")
counts: List[Int] = List(10, 20, 30)

As shown in the above:

Input: pairedData is a List[(String, Int)], which corresponds to F[(A, B)] where F is List, A is String, and B is Int.

Mechanism: Internally, distribute uses map twice:

map(pairedData)(_._1): Creates the List[String] (F[A]).
map(pairedData)(_._2): Creates the List[Int] (F[B]).

Output: The result is a tuple of two lists: (List[String], List[Int]), which corresponds to (F[A], F[B]). This is often useful when you receive combined data and need to separate it into parallel columns or streams.

Verifying Functor Laws: For example📝¹²

1. Identity Law: Mapping with the identity function returns the structure unchanged. $\text{map}(x)(\text{id}) = x$

where $\text{id}(a) = a$ for all $a$.

Translation: someList.map(x => x) == someList

2. Composition Law: Mapping with two composed functions is the same as mapping twice.

\[\text{map}(x)(g \circ f) = \text{map}(\text{map}(x)(f))(g)\]

where $(g \circ f)(x) = g(f(x))$ means “apply $f$ first, then apply $g$”.

def verifyFunctorIdentityLaw[F[_], A](fa: F[A])(implicit functor: Functor[F]): Boolean = {
  // Identity function
  def identity[X](x: X): X = x
  
  // map with identity should equal the original
  functor.map(fa)(identity) == fa
}

def verifyFunctorCompositionLaw[F[_], A, B, C](
  fa: F[A]
)(
  f: A => B, 
  g: B => C
)(implicit functor: Functor[F]): Boolean = {
  
  // Compose functions
  def composed(a: A): C = g(f(a))
  
  // map(map(fa)(f))(g) should equal map(fa)(g ∘ f)
  val leftSide = functor.map(functor.map(fa)(f))(g)
  val rightSide = functor.map(fa)(composed)
  
  leftSide == rightSide
}

defined function verifyFunctorIdentityLaw
defined function verifyFunctorCompositionLaw

Example:Option Functor:

trait Functor[F[_]] {
  def map[A,B](fa: F[A])(f: A => B): F[B]
}

val optFunctor: Functor[Option] = new Functor[Option] { //anonymous cls
    def map[A, B](a: Option[A])(f: A => B): Option[B] = a match {
        case None => None
        case Some(v) => Some(f(v))
    }
}

defined trait Functor
optFunctor: Functor[Option] = ammonite.$sess.cmd0$Helper$$anon$1@21586c94

Test the above:

optFunctor.map(Some(3))(n => n *2)

res1: Option[Int] = Some(value = 6)

Example: Function Functor:

Functions can be functors too! This is one of the most mind-bending examples:

trait Functor[F[_]] {
  def map[A, B](fa: F[A])(f: A => B): F[B]
}

// FunFunctor[I] creates a Functor instance for function types `I => _`
def FunFunctor[I]: Functor[({type L[X] = I => X})#L] = new Functor[({type L[X] = I => X})#L] { // ✔️
    //map takes a function `g: I => A` and composes it with `f: A => B`
    def map[A, B](g: I => A)(f: A => B): I => B = {
      (input: I) => f(g(input))
    }
  }

defined trait Functor
defined function FunFunctor

✔️ To function type parameterised by the return type, in Scala 2, Functor[({type L[X] = I => X})#L] can be written as Functor[I => *] in Scala 3.

Test it:

// Test it
val addOne: Int => Int = _ + 1
val intToString: Int => String = _.toString

val functor = FunFunctor[Int]
val composed = functor.map(addOne)(intToString)
composed(5)

addOne: Int => Int = ammonite.$sess.cmd7$Helper$$Lambda$2490/0x000000012883ca08@2acc74a3
intToString: Int => String = ammonite.$sess.cmd7$Helper$$Lambda$2491/0x000000012883c400@38a26a37
functor: Functor[[X]Int => X] = ammonite.$sess.cmd4$Helper$$anon$1@2becf695
composed: Int => String = ammonite.$sess.cmd4$Helper$$anon$1$$Lambda$2479/0x000000012883e220@4d95772
res7_4: String = "6"

Same as above

val f1 = FunFunctor[String].map(_.toInt + 2)(_ * 3.1)
f1("5")

f1: String => Double = ammonite.$sess.cmd4$Helper$$anon$1$$Lambda$2479/0x000000012883e220@3cee1dd7
res25_1: Double = 21.7

Lifting function examples

Functors let you lift¹³ ordinary functions to work with containers:

trait Functor[F[_]] {
    def map[A, B](fa: F[A])(f: A => B): F[B]
}

// Implicit Functor instance for Option
implicit val optionFunctor: Functor[Option] = new Functor[Option] {
    def map[A, B](fa: Option[A])(f: A => B): Option[B] = fa.map(f)
}

// Lifting function
def lift[F[_], A, B](f: A => B)(implicit functor: Functor[F]): F[A] => F[B] = {
    c => functor.map(c)(f)
}

defined trait Functor
optionFunctor: Functor[Option] = ammonite.$sess.cmd0$Helper$$anon$1@6632212a
defined function lift

Examples for the lifting function:

// Lift a simple function to work with Options
val addFive: Int => Int = _ + 5
val addFiveToOption: Option[Int] => Option[Int] = lift(addFive)

addFiveToOption(Some(10))  // Some(15)
addFiveToOption(None)      // None

addFive: Int => Int = ammonite.$sess.cmd1$Helper$$Lambda$2063/0x00000001297c0418@3e26e549
addFiveToOption: Option[Int] => Option[Int] = ammonite.$sess.cmd0$Helper$$Lambda$2064/0x00000001297c0800@696bf759
res1_2: Option[Int] = Some(value = 15)
res1_3: Option[Int] = None

Alternative: Using a companion object For better organisation, you could also place implicit instances in the Functor companion object:

trait Functor[F[_]] {
    def map[A, B](fa: F[A])(f: A => B): F[B]
}

// provide an implementation of Functor for Option.
object Functor {
    // Implicit Functor instance for Option
    implicit val optionFunctor: Functor[Option] = new Functor[Option] {
      def map[A, B](fa: Option[A])(f: A => B): Option[B] = fa.map(f)
    }
}

// Rest of the code remains the same

// Lifting function
def lift[F[_], A, B](f: A => B)(implicit functor: Functor[F]): F[A] => F[B] = {
    c => functor.map(c)(f)
}
val addFive: Int => Int = _ + 5
val addFiveToOption: Option[Int] => Option[Int] = lift(addFive)

// Lift a simple function to work with Options
addFiveToOption(Some(10))  // Some(15)
addFiveToOption(None)      // None

defined trait Functor
defined object Functor
defined function lift
addFive: Int => Int = ammonite.$sess.cmd0$Helper$$Lambda$2022/0x00000001327a8620@62d39784
addFiveToOption: Option[Int] => Option[Int] = ammonite.$sess.cmd0$Helper$$Lambda$2023/0x00000001327ab220@935ddf5
res0_5: Option[Int] = Some(value = 15)
res0_6: Option[Int] = None

Functor isn’t too compelling, as there aren’t many useful operations that can be defined purely in terms of map.

Applicative

Overview

An Applicative Functor (or just “Applicative”) extends Functor with the ability to:

Wrap a pure value in a context (pure)
Apply functions that are themselves in a context (ap)

Applicative functors are less powerful than monads, but more general (and hence more common). Think of it as a Functor with “superpowers” for combining multiple independent effects.¹⁴

With Applicative, you can combine multiple independent computations. You don’t need the result of one to determine the next (unlike Monad).¹⁵

---
config:
  look: neo
  theme: default
---
graph TD
    A["F[A]"] --> D["F[C]"]
    B["F[B]"] --> D
    C["(A, B) => C"] --> D
    
    E[Applicative] --> F[pure: Wrap values]
    E --> G[map2: Combine two contexts]
    E --> H[apply: Apply wrapped functions]
    
    style A fill:#2196F3
    style B fill:#2196F3
    style D fill:#4CAF50
    style C fill:#FF9800
    style E fill:#9C27B0

Applicative combines multiple independent contexts using a function, producing a result in a combined context. Imagine you’re a chef with ingredients in different boxes:

Functor: You can transform one ingredient at a time
- map(sugar)(addSpice) → spiced sugar
Applicative: You can combine multiple ingredients using a recipe (function)
- You have: F[Sugar], F[Flour], F[Eggs]
- Recipe: (sugar, flour, eggs) => Cake
- Applicative lets you combine them: F[Cake]

Applicative Mathematics

Formal Definition: An applicative functor consists of:

A type constructor $F: \text{Type} \to \text{Type}$
Operations:
- $\text{pure}: A \to F[A]$ — wraps a pure value in the context
- $\text{map2}: (F[A], F[B], (A, B) \to C) \to F[C]$ — combines two contexts
- Alternatively: $\text{ap}: F[A \to B] \to F[A] \to F[B]$ — applies a wrapped function

Mathematical Notation for ap:

\[\text{ap}: F[A \to B] \times F[A] \to F[B]\]

Translation: ap takes a function wrapped in context $F$ and a value wrapped in context $F$, and produces a result wrapped in $F$.¹⁶

Applicative Laws:

1. Identity Law: Applying the identity function wrapped in $F$ does nothing.

\[\text{ap}(\text{pure}(\text{id}))(v) = v\]

2. Homomorphism Law: Wrapping and then applying is the same as applying then wrapping.

\[\text{ap}(\text{pure}(f))(\text{pure}(x)) = \text{pure}(f(x))\]

3. Interchange Law: Order of applying functions doesn’t matter.

\[\text{ap}(u)(\text{pure}(y)) = \text{ap}(\text{pure}(f \mapsto f(y)))(u)\]

4. Composition Law: Composing applications is the same as applying compositions.

\[\text{ap}(\text{ap}(\text{ap}(\text{pure}(\text{compose}))(u))(v))(w) = \text{ap}(u)(\text{ap}(v)(w))\]

where $\text{compose}(f)(g)(x) = f(g(x))$.¹⁷

Scala Implementation

Type Class Definition:¹⁸

Monad

Overview

A Monad is the most powerful of these abstractions. It extends Applicative with the ability to sequence computations where each step can depend on the results of previous steps. The key operation is flatMap (also called bind or >>=).¹⁹

With Monad, later computations can depend on earlier results. This is more powerful than Applicative but also more restrictive (monads don’t compose as nicely).²⁰

---
config:
  look: neo
  theme: default
---
graph TD
    A["value: A"] -->|"pure"| B["F[A]"]
    B -->|"flatMap<br/>(f: A => F[B])"| C["F[B]"]
    C -->|"flatMap<br/>(g: B => F[C])"| D["F[C]"]
    
    E[Monad Hierarchy]
    E --> F[Monad]
    F --> G[Applicative]
    G --> H[Functor]
    
    style A fill:#FF9800
    style B fill:#2196F3
    style C fill:#4CAF50
    style D fill:#9C27B0
    style F fill:#F44336

Monads sequence dependent computations. Each step produces a context F[_], and flatMap chains them together. Every Monad is also an Applicative and Functor. Let you sequence operations with custom behaviour:

Option Monad: Stop on first None (short-circuit on failure)
List Monad: Generate all combinations (non-deterministic computation)
Future Monad: Wait for async results (sequencing async operations)
State Monad: Thread state through computations

Formal Definition: A monad consists of:

A type constructor $M: \text{Type} \to \text{Type}$ Wraps a plain value into the monadic context
Two operations:
- $\text{pure}: A \to M[A]$ — wrap a value (also called unit or return)
  Signature: def unit[A](a: => A): F[A]
- $\text{flatMap}: M[A] \times (A \to M[B]) \to M[B]$ — sequence computations
  Signature: def flatMap[A,B](fa: F[A])(f: A => F[B]): F[B]

Alternative Definition using join:

A monad can also be defined with:

$\text{pure}: A \to M[A]$
$\text{join}: M[M[A]] \to M[A]$ — flatten nested contexts
$\text{map}: M[A] \times (A \to B) \to M[B]$ — from Functor

The two definitions are equivalent: $\text{flatMap}(ma)(f) = \text{join}(\text{map}(ma)(f))$ $\text{join}(mma) = \text{flatMap}(mma)(\text{id})$

Category Theory Foundation:

In category theory, a monad $(T, \eta, \mu)$ on a category $\mathcal{C}$ consists of:

An endofunctor $T: \mathcal{C} \to \mathcal{C}$ (the type constructor)
A natural transformation $\eta: \text{Id} \to T$ (pure/unit)
A natural transformation $\mu: T \circ T \to T$ (join)

Translation: In Scala, $T$ is our type constructor like Option[_] or List[_], $\eta$ is pure, and $\mu$ is join.²¹

Monadic Combinators

Definition: Combinators are functions that work generically across any monad F[_], abstracting common patterns for combining and transforming monadic values.

Key monadic combinators:

sequence: Convert List[F[A]] to F[List[A]] — flip a list of effects into an effect containing a list
traverse: Apply a function A => F[B] to each element and collect results — map followed by sequence
replicateM: Repeat a monadic computation n times and collect results
filterM: Filter with a monadic predicate A => F[Boolean]
map2: Combine two monadic values with a binary function
product: Combine two monadic values into a tuple

These functions are implemented once in the Monad trait and inherited by all monadic types.

Monadic Types

Definition: Types that provide flatMap and unit operations, satisfying the monad laws.

Common monadic types in Scala:

Type	Context/Meaning	Example
`Option[A]`	Computation may fail (no error message)	`Some(5)`, `None`
`Either[E, A]`	Computation may fail with error message	`Right(5)`, `Left("error")`
`Try[A]`	Exception handling	`Success(5)`, `Failure(exception)`
`List[A]`	Non-determinism (multiple results)	`List(1, 2, 3)`
`Future[A]`	Asynchronous computation	`Future { computation }`
`State[S, A]`	Stateful computation	`State(s => (value, newState))`
`Par[A]`	Parallel computation	For parallel execution
`Parser[A]`	Parsing input	Sequential parsing operations

Monad Laws:

1. Left Identity: Wrapping a value and then flatMapping is the same as just applying the function.

\[\text{flatMap}(\text{pure}(a))(f) = f(a)\]

Translation: Option(x).flatMap(f) == f(x)

2. Right Identity: flatMapping with pure does nothing.

\[\text{flatMap}(m)(\text{pure}) = m\]

Translation: m.flatMap(x => Option(x)) == m

3. Associativity: The order of nesting flatMaps doesn’t matter.

\[\text{flatMap}(\text{flatMap}(m)(f))(g) = \text{flatMap}(m)(x \Rightarrow \text{flatMap}(f(x))(g))\]

Translation: m.flatMap(f).flatMap(g) == m.flatMap(x => f(x).flatMap(g))²²

Scala Implementation

trait Functor[F[_]] {
  def map[A, B](fa: F[A])(f: A => B): F[B]
}

trait Applicative[F[_]] extends Functor[F] {
  def pure[A](value: A): F[A]
  def map2[A, B, C](fa: F[A], fb: F[B])(f: (A, B) => C): F[C]
}

// Monad extends Applicative
trait Monad[F[_]] extends Applicative[F] {
  // The key operation: sequence dependent computations
  def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B]
  
  // join can be implemented using flatMap
  // def join[A](nestedContext: F[F[A]]): F[A] = {
  //   flatMap(nestedContext)(innerContext => innerContext)
  // }
  
  // map can be implemented using flatMap and pure
  override def map[A, B](fa: F[A])(f: A => B): F[B] = {
    flatMap(fa)(a => pure(f(a)))
  }
  
  // map2 can be implemented using flatMap
  override def map2[A, B, C](fa: F[A], fb: F[B])(f: (A, B) => C): F[C] = {
    flatMap(fa) { a =>
      map(fb) { b =>
        f(a, b)
      }
    }
  }
}

defined trait Functor
defined trait Applicative
defined trait Monad

implicit val listMonad: Monad[List] = new Monad[List] {
  def pure[A](value: A): List[A] = List(value)
  
  def flatMap[A, B](fa: List[A])(f: A => List[B]): List[B] = 
    fa.flatMap(f)
}

// Usage: Generate all combinations
val sizes = List("S", "M", "L")
val colors = List("Red", "Blue", "Green")

val products = listMonad.flatMap(sizes) { size =>
  listMonad.map(colors) { color =>
    s"$color $size T-Shirt"
  }
}

listMonad: Monad[List] = ammonite.$sess.cmd2$Helper$$anon$1@220ae3d8
sizes: List[String] = List("S", "M", "L")
colors: List[String] = List("Red", "Blue", "Green")
products: List[String] = List(
  "Red S T-Shirt",
  "Blue S T-Shirt",
  "Green S T-Shirt",
  "Red M T-Shirt",
  "Blue M T-Shirt",
  "Green M T-Shirt",
  "Red L T-Shirt",
  "Blue L T-Shirt",
  "Green L T-Shirt"
)

trait Functor[F[_]] {
    def map[A, B](fa: F[A])(f: A => B): F[B]
}

trait Monad[F[_]] extends Functor[F] {
    def unit[A](a: => A): F[A]
    def flatMap[A, B](ma: F[A])(f: A => F[B]): F[B]

    def map[A, B](ma: F[A])(f: A => B): F[B] = flatMap(ma)(a => unit(f(a)))
    def map[A, B, C](ma: F[A], mb: F[B])(f: (A, B) => C): F[C] = flatMap(ma)(a => map(mb)(b => f(a,b)))
}

defined trait Functor
defined trait Monad

References

Functional Programming in Scala, Ch. 10: “Monoids” - Introduction to purely algebraic structures ↩
Scala with Cats, Ch. 2: “Monoids and Semigroups” - Definition of Semigroup ↩
Functional Programming in Scala, Ch. 10.3: “Parallelism and Monoids” - Associativity enables parallel computation ↩
Scala with Cats, Ch. 2.2: “Definition of a Semigroup” - Scala implementation ↩ ↩² ↩³
Scala with Cats, Ch. 2.1: “Definition of a Monoid” - Example of non-associative operation ↩
Scala with Cats, Ch. 2.1: “Definition of a Monoid” - Formal monoid definition ↩
Functional Programming in Scala, Ch. 10.1: “What is a monoid?” - Intuition and examples ↩
Scala with Cats, Ch. 2.1: “Definition of a Monoid” - Type class definition ↩
Functional Programming in Scala, Ch. 10.3: “Parallelism and monoids” - Parallel reduction with monoids ↩
Scala with Cats, Ch. 2.2: “Definition of a Semigroup” - NonEmptyList example ↩
Functional Programming in Scala, Ch. 11.1: “Functors: generalizing the map function” - Functor introduction ↩
Functional Programming in Scala, Ch. 11.1.1: “Functor laws” - Identity and composition laws ↩
Functional Programming in Scala, Ch. 11.1: “Functors” - Lifting functions ↩
Functional Programming in Scala, Ch. 12.2: “The Applicative trait” - Introduction to Applicative ↩
Functional Programming in Scala, Ch. 12.3: “The difference between monads and applicative functors” - Independence of effects ↩
Functional Programming in Scala, Ch. 12.2 (Exercise 12.2): “Alternative Applicative definition” - ap method ↩
Functional Programming in Scala, Ch. 12.5: “The applicative laws” - Formal law definitions ↩
Functional Programming in Scala, Ch. 12.2: “The Applicative trait” - Type class definition ↩
Functional Programming in Scala, Ch. 11.2: “Monads: generalizing the flatMap and unit functions” - Monad introduction ↩
Functional Programming in Scala, Ch. 12.3: “The difference between monads and applicative functors” - Monad vs Applicative ↩
Category Theory for Programmers, Ch. 22: “Monads” - Category theory definition ↩
Functional Programming in Scala, Ch. 11.4: “Monad laws” - Formal law definitions ↩