Scala 2 Functors explaned

This comprehensive guide explores Scala 2 Functors, one of functional programming's fundamental abstractions rooted in category theory. Learn how Functors enable transforming values within computational contexts like List, Option, Either, and Future without leaving that context. The article covers mathematical foundations, including categories, objects, and morphisms, then demonstrates practical Scala implementations with concrete examples. Discover the Functor trait's map operation, understand identity and composition laws, and explore advanced concepts like contravariant functors and functor composition. Perfect for Scala developers seeking to master functional programming patterns, this guide bridges theoretical category theory with real-world Scala code examples and best practices.
- Introduction
- Mathematical Foundations
- Functor in Category Theory
- Functors in Scala 2
- Functor Laws
- Practical Examples
- Advanced Topics
- Summary
Introduction
A Functor is one of the most fundamental abstractions in functional programming. Before diving into Scala code, let’s understand the concept intuitively:
Intuitive Definition: A Functor is a computational context (like
List,Option,Future) that allows you to apply a function to values inside that context without leaving the context.
Think of it like this: If you have a gift box (context) with a toy inside, a Functor lets you replace that toy with a different one without opening the box. You just describe the transformation, and the Functor handles applying it within the box.
Mathematical Foundations
Category Theory Basics
Before understanding Functors, we need to understand categories.
What is a Category?
---
config:
look: neo
theme: default
---
graph LR
A[Object A] -->|arrow f| B[Object B]
B -->|arrow g| C[Object C]
A -->|arrow g ∘ f| C
style A fill:#e1f5ff
style B fill:#e1f5ff
style C fill:#e1f5ff
In Category Theory, we talk about “Categories,” “Objects,” and “Morphisms” (arrows). In Scala 2, we translate these concepts directly into programming constructs:
- Objects become Types (e.g.,
Int,String,User). - Morphisms become Functions (e.g.,
Int => String). - Composition is the ability to glue functions together.
1. The Category of Scala Types (Composition)
In a category, if you have an arrow from A to B, and an arrow from B to C, you must be able to compose them to get an arrow from A to C.
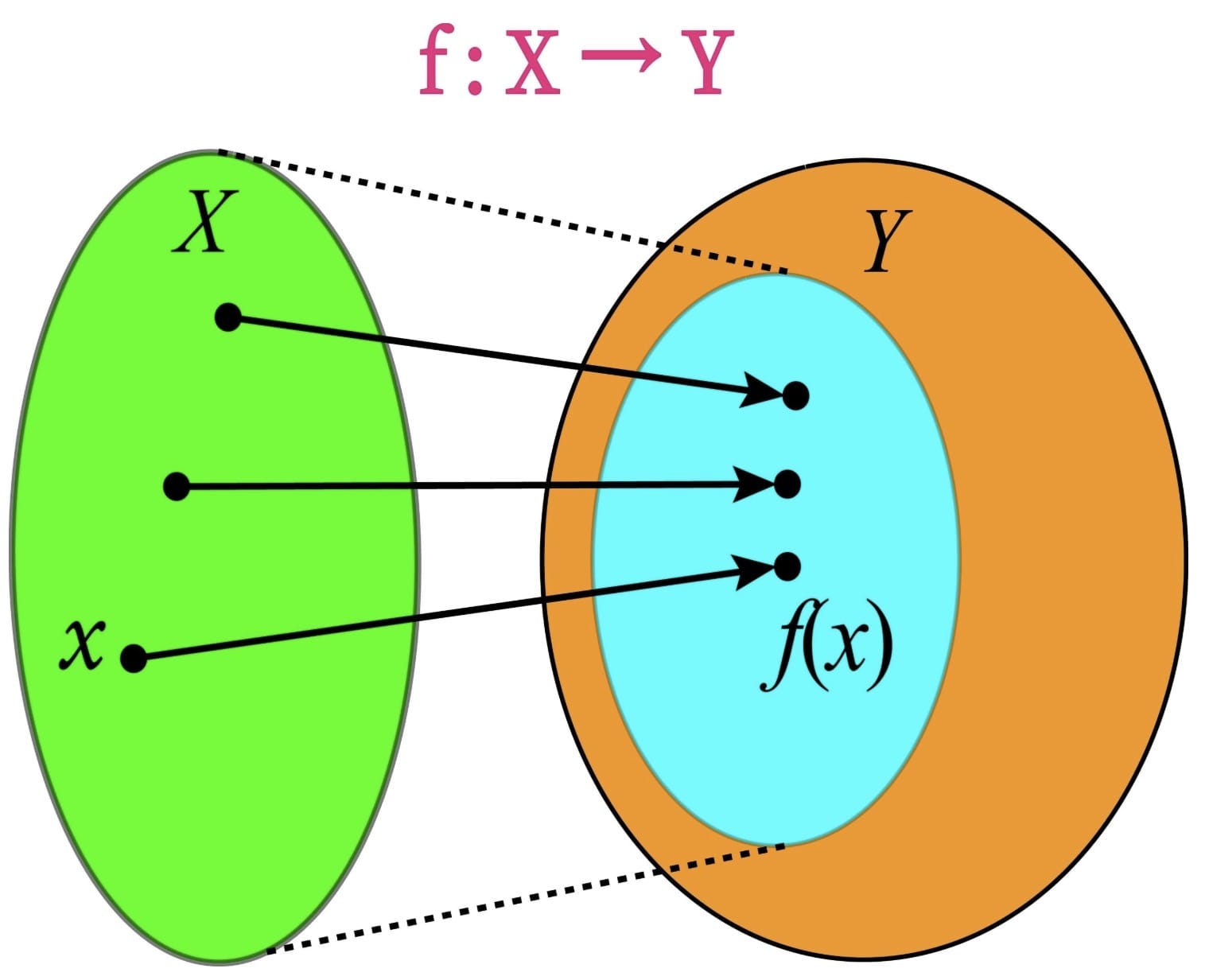
If $f: A \rightarrow B$ and $g: B \rightarrow C$, then $g \circ f: A \rightarrow C$.
// Morphism 1: A -> B (Int to Double)
val intToDouble: Int => Double = i => i.toDouble
// Morphism 2: B -> C (Double to String)
val doubleToString: Double => String = d => s"Value is $d"
// Composition: A -> C (Int to String)
// Scala uses 'andThen' or 'compose' to glue these arrows together
val intToString: Int => String = intToDouble.andThen(doubleToString)
intToString(5)
// Output: Value is 5.0
intToDouble: Int => Double = ammonite.$sess.cmd0$Helper$$Lambda$1975/0x0000000800ab4040@2d5eeb02
doubleToString: Double => String = ammonite.$sess.cmd0$Helper$$Lambda$1976/0x0000000800ab5040@2409f782
intToString: Int => String = scala.Function1$$Lambda$740/0x0000000800673040@3b91088
res0_3: String = "Value is 5.0"
Mathematical Definition: A category $\mathcal{C}$ consists of:1
- Objects: $A, B, C, \ldots$ (think of these as types)
- Arrows (morphisms): $f : A \to B$ (think of these as functions)
- Identity arrows: For every object $A$, there exists $1_A : A \to A$
- Composition: For arrows $f : A \to B$ and $g : B \to C$, there exists $g \circ f : A \to C$
Laws:
- Associativity: $h \circ (g \circ f) = (h \circ g) \circ f$
- Identity: $f \circ 1_A = f$ and $1_B \circ f = f$
Notation Guide:
- $\circ$ means “composed with” (like the dot in math)
- $A \to B$ means “an arrow from A to B”
- $1_A$ means “identity arrow for object A”
Examples of Categories
- Set (Category of Sets):
- Objects: All sets
- Arrows: Functions between sets
- Scala (Category of Scala Types):
- Objects: Scala types (
Int,String,List[A], etc.) - Arrows: Scala functions (
A => B)
- Objects: Scala types (
Functor in Category Theory
A Functor is a mapping between categories that preserves structure. Think of a Functor as a Container (or Context) that holds a value, where you can apply a function to the value inside without taking it out of the container.
The tell-tale sign of a Functor in Scala is the
.mapmethod.List,Option, andFutureare all Functors.
Formal Definition
---
config:
look: neo
theme: default
---
graph TB
subgraph "Category C"
A[Object A] -->|f| B[Object B]
end
subgraph "Category D"
FA[F A] -->|F f| FB[F B]
end
A -.->|Functor F| FA
B -.->|Functor F| FB
style A fill:#e1f5ff
style B fill:#e1f5ff
style FA fill:#ffe1f5
style FB fill:#ffe1f5
Mathematical Definition: A functor $F : \mathcal{C} \to \mathcal{D}$ between categories $\mathcal{C}$ and $\mathcal{D}$ consists of:1
- Object mapping: For each object $A$ in $\mathcal{C}$, an object $F(A)$ in $\mathcal{D}$
- Arrow mapping: For each arrow $f : A \to B$ in $\mathcal{C}$, an arrow $F(f) : F(A) \to F(B)$ in $\mathcal{D}$
Such that:
- Preserves identity: \(F(1_A) = 1_{F(A)}\)
- Preserves composition: $F(g \circ f) = F(g) \circ F(f)$
A Functor is a “structure-preserving map” between categories. It maps objects to objects and arrows to arrows while preserving the categorical structure.
Endofunctor
In programming, we typically work with endofunctors—functors from a category to itself.
\[F : \mathcal{Scala} \to \mathcal{Scala}\]For example:
Listis a functor: it maps typeAto typeList[A]Optionis a functor: it maps typeAto typeOption[A]
Functors in Scala 2
The Functor Trait
Here’s the Scala 2 definition of a Functor:2
trait Functor[F[_]] {
def map[A, B](fa: F[A])(f: A => B): F[B]
}
defined trait Functor
F[_]is a type constructor (takes a type and produces a type)mapis the only required operationmapapplies functionf: A => Bto values inside contextF[A]to produceF[B]
Type Constructor Explanation
// F[_] means "F takes one type parameter"
List // F in List[A]
Option // F in Option[A]
Either[E, _] // Can be partially applied to get F[_]
Functor Instances
List Functor
This example creates a listFunctor instance by implementing the Functor[List] trait. The map method delegates to List’s built-in map function, demonstrating that Scala’s List already has functor-like behavior. The example shows transforming [1, 2, 3] to [2, 4, 6] by applying _ * 2, maintaining the List context throughout the transformation.
// Creating a Functor instance for List
val listFunctor = new Functor[List] {
def map[A, B](as: List[A])(f: A => B): List[B] =
as.map(f) // Uses built-in List.map
}
// Example usage
val numbers = List(1, 2, 3)
val doubled = listFunctor.map(numbers)(_ * 2)
// doubled = List(2, 4, 6)
listFunctor: AnyRef with Functor[List] = ammonite.$sess.cmd1$Helper$$anon$1@17ebf35a
numbers: List[Int] = List(1, 2, 3)
doubled: List[Int] = List(2, 4, 6)
Source: 2 : Shows how to create a concrete Functor instance that works with Scala’s List type, bridging the gap between abstract category theory and practical Scala programming.
This code exemplifies the category theory concept where:
- Object mapping:
Int→List[Int] - Arrow mapping: function
f: A => B→map(f): List[A] => List[B] - Preserves structure: The List context is maintained throughout the transformation
This is the first concrete example showing that familiar Scala collections like List are actually functors that satisfy the mathematical laws (identity and composition) discussed earlier in the notebook. It makes the abstract theory tangible by using everyday Scala code.
Option Functor
---
config:
look: classic
theme: default
---
classDiagram
class Option~A~ {
<<abstract>>
+isEmpty: Boolean
+isDefined: Boolean
+get: A
+getOrElse(default: => A): A
+orElse(alternative: => Option[A]): Option[A]
+map[B](f: A => B): Option[B]
+flatMap[B](f: A => Option[B]): Option[B]
+filter(p: A => Boolean): Option[A]
+foreach(f: A => Unit): Unit
+fold[B](ifEmpty: => B)(f: A => B): B
+contains(elem: A): Boolean
+exists(p: A => Boolean): Boolean
+forall(p: A => Boolean): Boolean
}
class Some~A~ {
+value: A
+isEmpty: Boolean = false
+isDefined: Boolean = true
+get: A
}
class None {
+isEmpty: Boolean = true
+isDefined: Boolean = false
+get: Nothing
}
Option <|-- Some : extends
Option <|-- None : extends
note for Option "Represents optional values
Instances are either Some(value) or None"
note for Some "Wraps a definite value"
note for None "Singleton object - no value"
// Option Functor
val optionFunctor = new Functor[Option] {
def map[A, B](optA: Option[A])(f: A => B): Option[B] = optA match {
case Some(value) => Some(f(value)) // Apply f to the value
case None => None // Preserve None
}
}
optionFunctor: AnyRef with Functor[Option] = ammonite.$sess.cmd6$Helper$$anon$1@20762413
// Example usage
val maybeAge: Option[Int] = Some(25)
optionFunctor.map(maybeAge)(_ >= 21)
// canDrink = Some(true)
maybeAge: Option[Int] = Some(value = 25)
res7_1: Option[Boolean] = Some(value = true)
val noAge: Option[Int] = None
optionFunctor.map(noAge)(_ >= 21)
// result = None
noAge: Option[Int] = None
res8_1: Option[Boolean] = None
Source: 2: The optionFunctor implements Functor[Option] using pattern matching. When the Option is Some(value), it applies function f to the value and wraps it back in Some. When it’s None, it preserves None without applying the function. This demonstrates safe computation - transformations only apply when a value exists. The examples show checking drinking age eligibility: Some(25) becomes Some(true), while None remains None, elegantly handling the absence of data without null pointer exceptions.
Type Constructor Hierarchy
---
config:
look: neo
theme: default
---
graph TD
A["Type Constructor F[_]"] --> B["Functor F[_]"]
B --> C["Applicative F[_]"]
C --> D["Monad F[_]"]
B --> E[map operation]
C --> F[map2, pure operations]
D --> G[flatMap, unit operations]
style A fill:#e1f5ff
style B fill:#ffe1e1
style C fill:#e1ffe1
style D fill:#ffe1f5
Functor Laws
Functors must satisfy two laws to be “well-behaved”:2
Law 1: Identity
Mathematical form: \(\text{map}(x)(\text{id}) = x\)
Where $\text{id}$ is the identity function: $\text{id}(a) = a$
// For any fa: F[A]
fa.map(a => a) == fa
// Or equivalently
fa.map(identity) == fa
Why this matters: Mapping with the identity function shouldn’t change the structure or its contents. This ensures map preserves structure.
val numbers = List(1, 2, 3)
// These are equivalent
numbers.map(x => x) // List(1, 2, 3)
numbers.map(identity) // List(1, 2, 3)
numbers // List(1, 2, 3)
numbers: List[Int] = List(1, 2, 3)
res9_1: List[Int] = List(1, 2, 3)
res9_2: List[Int] = List(1, 2, 3)
res9_3: List[Int] = List(1, 2, 3)
Law 2: Composition
Mathematical form: \(\text{map}(x)(g \circ f) = \text{map}(\text{map}(x)(f))(g)\)
Where $(g \circ f)(x) = g(f(x))$
In Scala:
// For any fa: F[A] and functions f: A => B, g: B => C
fa.map(f).map(g) == fa.map(g compose f)
// Or equivalently:
fa.map(f).map(g) == fa.map(x => g(f(x)))
Why this matters: We can compose functions first, then map, or map twice—the result is the same. This lets us reason about code transformations algebraically.
val numbers = List(1, 2, 3)
val addOne: Int => Int = _ + 1
val double: Int => Int = _ * 2
// Two ways to do the same thing:
numbers.map(addOne).map(double) // List(4, 6, 8)
numbers.map(x => double(addOne(x))) // List(4, 6, 8)
numbers.map(double compose addOne) // List(4, 6, 8)
numbers: List[Int] = List(1, 2, 3)
addOne: Int => Int = ammonite.$sess.cmd5$Helper$$Lambda$2236/0x000000012780d6d8@228cdff9
double: Int => Int = ammonite.$sess.cmd5$Helper$$Lambda$2237/0x000000012780dac0@31a2695f
res5_3: List[Int] = List(4, 6, 8)
res5_4: List[Int] = List(4, 6, 8)
res5_5: List[Int] = List(4, 6, 8)
Law Verification Example
Let’s verify the laws for Option:
// Identity Law
val someValue: Option[Int] = Some(42)
assert(someValue.map(identity) == someValue)
val noneValue: Option[Int] = None
assert(noneValue.map(identity) == noneValue)
// Composition Law
val f: Int => Int = _ + 10
val g: Int => String = _.toString
assert(
someValue.map(f).map(g) ==
someValue.map(x => g(f(x)))
)
// Both produce: Some("42")
someValue: Option[Int] = Some(value = 42)
noneValue: Option[Int] = None
f: Int => Int = ammonite.$sess.cmd6$Helper$$Lambda$2253/0x00000001278118f8@630d0a41
g: Int => String = ammonite.$sess.cmd6$Helper$$Lambda$2254/0x0000000127811ce0@543024b9
Practical Examples
Example 1: Mapping Over Collections
// Transform a list of ages to determine eligibility
val ages: List[Int] = List(15, 21, 18, 30, 16)
// Using Functor abstraction
def isAdult(age: Int): Boolean = age >= 18
val eligibility: List[Boolean] = ages.map(isAdult)
// Result: List(false, true, true, true, false)
// Chain multiple transformations
val formattedResults: List[String] =
ages.map(isAdult) // List[Boolean]
.map(eligible => if (eligible) "✓" else "✗") // List[String]
// Result: List("✗", "✓", "✓", "✓", "✗")
ages: List[Int] = List(15, 21, 18, 30, 16)
defined function isAdult
eligibility: List[Boolean] = List(false, true, true, true, false)
formattedResults: List[String] = List("✗", "✓", "✓", "✓", "✗")
Functor Perspective: This example demonstrates the composition law in action. The chained transformations show that List functor preserves composition:
From category theory:
- Arrow mapping:
isAdult: Int => Booleanis lifted tomap(isAdult): List[Int] => List[Boolean] - Composition preserved: Two sequential
mapoperations compose into a single functor mapping - Context maintained: The
Listfunctor context $F(\text{age})$ is preserved through transformations:List[Int]→List[Boolean]→List[String]
This exemplifies how functors allow us to work with values inside a computational context without ever “unwrapping” them, maintaining type safety throughout the transformation pipeline.
Example 2: Safe Division with Option
// Division that returns Option to handle division by zero
def safeDivide(numerator: Int, denominator: Int): Option[Double] = {
if (denominator == 0) None
else Some(numerator.toDouble / denominator)
}
// Using map to transform the result
val result1: Option[Double] = safeDivide(10, 2).map(_ * 100)
// result1 = Some(500.0)
val result2: Option[Double] = safeDivide(10, 0).map(_ * 100)
// result2 = None (computation "short-circuits")
// Chaining transformations
val formattedResult: Option[String] =
safeDivide(15, 3)
.map(_ * 2) // Some(10.0)
.map(_.toInt) // Some(10)
.map(n => s"Result: $n") // Some("Result: 10")
defined function safeDivide
result1: Option[Double] = Some(value = 500.0)
result2: Option[Double] = None
formattedResult: Option[String] = Some(value = "Result: 10")
above code Inspired by: 3
Functor Perspective: The Option functor demonstrates safe computation with potential failure. From category theory:
Arrow Lifting: The function _ * 100: Double => Double is lifted to the Option context:
\(\text{map}: (\text{Double} \to \text{Double}) \to (\text{Option}[\text{Double}] \to \text{Option}[\text{Double}])\)
Short-Circuit Behavior: When safeDivide returns None (division by zero), subsequent map operations preserve None:
\(\text{map}(\text{None})(f) = \text{None} \quad \forall f\)
Composition Chain: The chained transformations show functor composition law: \(\begin{align} &\text{Option}[\text{Double}] \xrightarrow{\text{map}(\_ \times 2)} \text{Option}[\text{Double}] \\ &\xrightarrow{\text{map}(\_.toInt)} \text{Option}[\text{Int}] \\ &\xrightarrow{\text{map}(n \Rightarrow s)} \text{Option}[\text{String}] \end{align}\)
This exemplifies how the Option functor handles computational effects (potential absence of value) while maintaining the functor laws. The transformation pipeline remains type-safe and composable whether the value is Some or None.
Example 3: Lifting Functions
The map operation can be thought of as “lifting” a function into a context:2
// Functor trait
trait Functor[F[_]] {
def map[A, B](fa: F[A])(f: A => B): F[B]
}
// Implicit Functor instances
object Functor {
implicit val optionFunctor: Functor[Option] = new Functor[Option] {
def map[A, B](fa: Option[A])(f: A => B): Option[B] = fa.map(f)
}
implicit val listFunctor: Functor[List] = new Functor[List] {
def map[A, B](fa: List[A])(f: A => B): List[B] = fa.map(f)
}
}
import Functor._
// Lift converts A => B into F[A] => F[B]
def lift[F[_], A, B](f: A => B)(implicit F: Functor[F]): F[A] => F[B] =
fa => F.map(fa)(f)
defined trait Functor
defined object Functor
import Functor._
// Lift converts A => B into F[A] => F[B]
defined function lift
Source2 of above code:
- Implicit Instances - The Functor object defines implicit values (
optionFunctor,listFunctor) that provideFunctorimplementations for specific types. - Implicit Parameter - The
liftfunction has animplicit F: Functor[F]parameter. When you call lift, Scala automatically searches for a matching implicitFunctor[F]in scope. - Import -
import Functor._brings the implicit instances into scope, making them available for the compiler to find.
The lift function demonstrates the fundamental arrow mapping property of functors. From category theory:
Lifting Definition: For any functor $F$ and function $f: A \to B$, lifting transforms it into $F(f): F(A) \to F(B)$: \(\text{lift}(f) = \lambda fa. \, \text{map}(fa)(f)\)
This is precisely the arrow mapping from the functor definition, making it explicit as a first-class function.
Polymorphic Lifting: The lift function works for any functor $F$, demonstrating parametric polymorphism:
\(\text{lift}: \forall F, A, B. \, (A \to B) \to (F[A] \to F[B])\)
// Example: Lift math.abs into Option context
val absOption: Option[Double] => Option[Double] = lift(math.abs)
val someNegative: Option[Double] = Some(-3.14)
val result = absOption(someNegative)
// result = Some(3.14)
// Lift works with any Functor
val absList: List[Double] => List[Double] = lift(math.abs)
val negatives = List(-1.5, -2.5, -3.5)
val absolutes = absList(negatives)
absOption: Option[Double] => Option[Double] = ammonite.$sess.cmd11$Helper$$Lambda$2318/0x000000012c816d98@82dae8f
someNegative: Option[Double] = Some(value = -3.14)
result: Option[Double] = Some(value = 3.14)
absList: List[Double] => List[Double] = ammonite.$sess.cmd11$Helper$$Lambda$2318/0x000000012c816d98@1e3d09f0
negatives: List[Double] = List(-1.5, -2.5, -3.5)
absolutes: List[Double] = List(1.5, 2.5, 3.5)
Examples:
math.abs: Double => Doublelifted toOptioncontext: $\text{abs}: \text{Option}[\text{Double}] \to \text{Option}[\text{Double}]$- Same function lifted to
Listcontext: $\text{abs}: \text{List}[\text{Double}] \to \text{List}[\text{Double}]$
Key Insight: Lifting transforms ordinary functions into context-aware functions without changing the function’s logic. The functor’s map operation handles the context (Option, List, etc.), while the lifted function focuses purely on the transformation. This separation of concerns is a core principle of functional programming.
Example 4: Parser Functor
From the “Functional Programming in Scala” book, we can define a Functor for parsers:2
// Functor trait
trait Functor[F[_]] {
def map[A, B](fa: F[A])(f: A => B): F[B]
}
// Parser that wraps a parsing function
case class Parser[+A](run: String => Option[(A, String)])
object ParserFunctor extends Functor[Parser] {
def map[A, B](parser: Parser[A])(f: A => B): Parser[B] = {
Parser { input =>
parser.run(input).map { case (a, remaining) =>
(f(a), remaining)
}
}
}
}
defined trait Functor
defined class Parser
defined object ParserFunctor
Above case class:
- Wraps a parsing function that processes string input
- The
runfunction signature:- Input:
String- the text to parse - Output:
Option[(A, String)]Some((value, remaining))- successful parse with extracted value and remaining inputNone- parse failure
- Input:
The ParserFunctor object:
- Takes a
Parser[A]and a transformation functionf: A => B - Returns a new
Parser[B]that:- Runs the original parser on the input
- If successful, applies
fto transform the parsed value fromAtoB - Preserves the remaining unparsed string unchanged
- Propagates failures (returns
Noneif original parser fails)
// Example integer parser
val intParser: Parser[Int] = Parser { input =>
input.takeWhile(_.isDigit) match {
case "" => None
case digits => Some((digits.toInt, input.drop(digits.length)))
}
}
intParser: Parser[Int] = Parser(
run = ammonite.$sess.cmd17$Helper$$Lambda$3421/0x0000000127acbec0@6bfbdf88
)
Above intParser:
Parser { input => ... }- Creates a new
Parser[Int]instance - The lambda defines the parsing logic for the
runfunction
- Creates a new
input.takeWhile(_.isDigit)- Extracts consecutive digit characters from the start of the input
- Stops at the first non-digit character
- Returns a string of digits (or empty string if input starts with non-digit)
- Pattern Matching
match { ... }Returns:
- Empty string: Parser fails, returns
None - Non-empty digits:
- Converts digit string to
Intusing.toInt - Drops parsed characters from input to get remaining string
- Returns
Some((parsedInt, remaining))
- Converts digit string to
- Empty string: Parser fails, returns
Here the examples:
// Transform to string
val stringParser: Parser[String] =
ParserFunctor.map(intParser)(_.toString)
// Check if even
val boolParser: Parser[Boolean] =
ParserFunctor.map(intParser)(_ % 2 == 0)
// Test examples
intParser.run("123abc") // Some((123, "abc"))
stringParser.run("456def") // Some(("456", "def"))
boolParser.run("8xyz") // Some((true, "xyz"))
stringParser: Parser[String] = Parser(
run = ammonite.$sess.cmd12$Helper$ParserFunctor$$$Lambda$2486/0x00000001278526f0@2998a456
)
boolParser: Parser[Boolean] = Parser(
run = ammonite.$sess.cmd12$Helper$ParserFunctor$$$Lambda$2486/0x00000001278526f0@5853148d
)
res18_2: Option[(Int, String)] = Some(value = (123, "abc"))
res18_3: Option[(String, String)] = Some(value = ("456", "def"))
res18_4: Option[(Boolean, String)] = Some(value = (true, "xyz"))
Advanced Topics
Relationship to Other Abstractions
---
config:
look: neo
theme: default
---
graph TB
F[Functor]
A[Applicative Functor]
M[Monad]
T[Traversable]
F --> A
A --> M
F --> T
A --> T
F -.->|"adds pure, map2"| A
A -.->|"adds flatMap"| M
F -.->|"adds traverse"| T
style F fill:#e1f5ff
style A fill:#ffe1f5
style M fill:#f5e1ff
style T fill:#e1ffe1
Functor vs Applicative vs Monad
| Abstraction | Operations | Power | When to Use |
|---|---|---|---|
| Functor | map |
Transform values in a context | Basic transformations, independent computations |
| Applicative | map2, pure |
Combine multiple contexts | Fixed structure, parallel operations |
| Monad | flatMap, unit |
Sequence computations, flatten nested contexts | Dependent computations, chaining operations |
Source: 4
Functor Composition
This code demonstrates functor composition - the ability to combine two functors to create a new functor that works on nested structures like List[Option[A]].
Functors compose! If F[_] and G[_] are functors, then F[G[_]] is also a functor:
// Functor trait
trait Functor[F[_]] {
def map[A, B](fa: F[A])(f: A => B): F[B]
}
defined trait Functor
- Provides functor implementations for
ListandOption - Marked
implicitso the compiler can find them automatically - Delegates to the built-in
.mapmethods
// Functor instances
implicit val listFunctor: Functor[List] = new Functor[List] {
def map[A, B](fa: List[A])(f: A => B): List[B] = fa.map(f)
}
implicit val optionFunctor: Functor[Option] = new Functor[Option] {
def map[A, B](fa: Option[A])(f: A => B): Option[B] = fa.map(f)
}
listFunctor: Functor[List] = ammonite.$sess.cmd16$Helper$$anon$1@7a4a3132
optionFunctor: Functor[Option] = ammonite.$sess.cmd16$Helper$$anon$2@51afcd91
- Creates a readable name for the nested type
List[Option[X]] - Makes code more self-documenting
- Not used directly in this example but shows what we’re working with
// Type alias instead of Lambda
type ListOption[X] = List[Option[X]]
defined type ListOption
Type Lambda: ({type L[X] = F[G[X]]})#L
- Scala 2 Type Lambda Syntax - a workaround for creating anonymous type constructors
- Defines a new type constructor
L[X]that representsF[G[X]] - The
#Lprojects out the type member - Equivalent to: “a functor for the composed type
F[G[_]]”
Constructor Parameters:
implicit F: Functor[F]- requires a functor instance for outer typeFimplicit G: Functor[G]- requires a functor instance for inner typeG
// Define a composed Functor
class ComposedFunctor[F[_], G[_]](
implicit F: Functor[F],
G: Functor[G]
) extends Functor[({type L[X] = F[G[X]]})#L] {
def map[A, B](fga: F[G[A]])(f: A => B): F[G[B]] = {
F.map(fga)(ga => G.map(ga)(f))
}
}
defined class ComposedFunctor
How it works:
- Takes a nested structure
F[G[A]](e.g.,List[Option[Int]]) - Uses outer functor
Fto map over the outer structure - For each inner value
ga: G[A], uses inner functorGto map over it - Applies transformation
f: A => Bto the innermost values - Returns
F[G[B]]with transformed values
Functor Perspective: This code demonstrates the crucial property that functors compose - a fundamental theorem in category theory.
Composition Theorem: If $F$ and $G$ are functors, then their composition $F \circ G$ is also a functor: \(F \circ G : \mathcal{C} \to \mathcal{C}\) \((F \circ G)(A) = F(G(A))\) \((F \circ G)(f) = F(G(f))\)
Implementation Details:
- Type-level composition:
F[G[X]]represents nested contexts (e.g.,List[Option[Int]]) - Map composition: To map over
F[G[A]], we:- Use $F$’s map to traverse the outer structure
- For each inner $G[A]$, use $G$’s map to apply function $f$
Mathematical Expression: \(\text{map}_{F \circ G}(f) = \text{map}_F(\text{map}_G(f))\)
In code: F.map(fga)(ga => G.map(ga)(f))
Functor Laws Preservation: The composed functor preserves both functor laws:
- Identity: $(F \circ G)(id) = F(G(id)) = F(id) = id$
- Composition: $(F \circ G)(g \circ f) = F(G(g \circ f)) = F(G(g) \circ G(f)) = F(G(g)) \circ F(G(f))$
This composition property allows building complex data structures (like List[Option[Int]]) that remain functorial, enabling safe and composable transformations.
// Example: List[Option[_]] is a Functor
val listOptionFunctor: Functor[ListOption] =
new ComposedFunctor[List, Option]
val data: List[Option[Int]] = List(Some(1), None, Some(3))
val doubled: List[Option[Int]] =
listOptionFunctor.map(data)((x: Int) => x * 2)
// Result: List(Some(2), None, Some(6))
listOptionFunctor: Functor[ListOption] = ammonite.$sess.cmd18$Helper$ComposedFunctor@5d0815b9
data: List[Option[Int]] = List(Some(value = 1), None, Some(value = 3))
doubled: List[Option[Int]] = List(Some(value = 2), None, Some(value = 6))
Contravariant Functor
This code demonstrates contravariance - a pattern that’s the “opposite” of regular functors. While functors produce values (covariant), contravariant functors consume values.
Some type constructors support a contramap operation instead of map:
trait Contravariant[F[_]] {
def contramap[A, B](fa: F[A])(f: B => A): F[B]
}
defined trait Contravariant
Key Difference from Functor
| Type | Signature | Direction |
|---|---|---|
| Functor | map[A, B](fa: F[A])(f: A => B): F[B] |
Forward: A => B |
| Contravariant | contramap[A, B](fa: F[A])(f: B => A): F[B] |
Backward: B => A |
Intuition:
- Functor: “I have
F[A], give me a way to getBfromA, I’ll give youF[B]” - Contravariant: “I have
F[A], give me a way to getAfromB, I’ll give youF[B]”
// Example: Show type class
trait Show[A] {
def show(a: A): String
}
implicit val showInt: Show[Int] = new Show[Int] {
def show(a: Int): String = a.toString
}
defined trait Show
showInt: Show[Int] = ammonite.$sess.cmd22$Helper$$anon$1@7578d5b5
The Show Type Class:
- Type class for converting values to strings
Show[A]is a consumer ofA(it takesAand producesString)- This makes it contravariant in
A
// We can create Show[Person] from Show[Int]
case class Person(age: Int)
implicit val showPerson: Show[Person] =
new Show[Person] {
def show(person: Person): String =
showInt.show(person.age)
}
defined class Person
showPerson: Show[Person] = ammonite.$sess.cmd23$Helper$$anon$1@56f63d52
Manual Implementation (Without Contramap):
- We have
Show[Int]- can show integers - We can extract an
IntfromPersonvia.age - Therefore, we can create
Show[Person]by: extract age → show the age
// Using contramap:
object ShowContravariant extends Contravariant[Show] {
def contramap[A, B](showA: Show[A])(f: B => A): Show[B] = {
new Show[B] {
def show(b: B): String = showA.show(f(b))
}
}
}
defined object ShowContravariant
ShowContravariant Implementation:
Type Parameters:
A= the type we already know how to show (e.g.,Int)B= the new type we want to show (e.g.,Person)
Parameters:
showA: Show[A]- existing Show instance for typeAf: B => A- function to convertBtoA
Return:
Show[B]- new Show instance for typeB
The Logic:
def show(b: B): String = showA.show(f(b))
// ↑ ↑ ↑
// input B show A convert B→A
- Take a value of type
B - Convert it to
Ausingf - Show the
Ausing existingshowA
val showPerson2: Show[Person] =
ShowContravariant.contramap(showInt)(_.age)
// ↑ ↑
// Show[Int] Person => Int
showPerson2: Show[Person] = ammonite.$sess.cmd24$Helper$ShowContravariant$$anon$1@709d0a62
As shown above elegent way is us Using Contramap:
- Map: “I’ll transform what comes OUT”
- Contramap: “I’ll transform what goes IN”
Visualization
Show[Int] ←──(contramap)── Show[Person] ←──(contramap)── Show[Employee]
↑ ↑ ↑
a.toString person.age employee.person
Data flows right to left (contravariant direction):
Employee → Person → Int → String
Contravariant Functor Perspective: While (covariant) functors use map, contravariant functors reverse the arrow direction using contramap.
Mathematical Definition: A contravariant functor $F : \mathcal{C}^{op} \to \mathcal{D}$ maps:
- Objects: $A \mapsto F(A)$
- Arrows reversed: $f: B \to A$ becomes $F(f): F(A) \to F(B)$
Notice the arrow reversal: $f: B \to A$ but $\text{contramap}(f): F[A] \to F[B]$
The Show Example: \(\text{Show}[\text{Int}] \xrightarrow{\text{contramap}(\text{Person} \to \text{Int})} \text{Show}[\text{Person}]\)
The function _.age: Person => Int goes from Person to Int, but contramap produces Show[Person] from Show[Int] - the type parameters are reversed!
Contravariant Functor Laws:
- Identity: $\text{contramap}(fa)(id) = fa$
- Composition: $\text{contramap}(fa)(f \circ g) = \text{contramap}(\text{contramap}(fa)(g))(f)$
Intuition: Contravariant functors represent consumers of data (like Show[A] consumes an A to produce a String). If you can convert B => A, you can adapt a consumer of A into a consumer of B by pre-composing the conversion:
This is the dual of covariant functors, which represent producers of data.
Summary
Key Takeaways
-
Functor Definition: A Functor is a type constructor
F[_]with amapoperation that transforms values inside a context without leaving the context. -
Mathematical Foundation: Functors come from category theory—they are structure-preserving mappings between categories.
- Functor Laws:
- Identity:
fa.map(identity) == fa - Composition:
fa.map(f).map(g) == fa.map(g compose f)
- Identity:
-
Common Examples:
List,Option,Either,Future,Parser,Gen - Power: Functors provide:
- Generic operations that work across different data types
- Function lifting
- Composition of computations
- Algebraic reasoning about programs
When to Use Functors
✅ Use Functors when:
- You need to transform values inside a context
- Transformations are independent (don’t depend on previous results)
- You want to lift ordinary functions into a context
- You need structure-preserving transformations
❌ Consider Applicative or Monad when:
- You need to combine multiple independent computations (
Applicative) - Computations depend on previous results (
Monad) - You need to flatten nested structures (
Monad)
Quick Reference Card
// Functor trait
trait Functor[F[_]] {
def map[A, B](fa: F[A])(f: A => B): F[B]
}
// Laws
fa.map(identity) == fa // Identity
fa.map(f).map(g) == fa.map(g compose f) // Composition
// Common instances
List[A] // listFunctor
Option[A] // optionFunctor
Either[E, A] // eitherFunctor (right-biased)
Future[A] // futureFunctor
Parser[A] // parserFunctor
-
Awodey, S. Category Theory. Oxford University Press, 2010. → Ch. 1: “Categories”, pp. 1-9, and Ch. 7: “Naturality”, pp. 147-150 ↩ ↩2
-
Chiusano, P. and Bjarnason, R. Functional Programming in Scala. Manning Publications, 2014. → Ch. 11: “Monads” → “Functors: generalizing the map function”, pp. 187-190 ↩ ↩2 ↩3 ↩4 ↩5 ↩6 ↩7
-
Chiusano, P. and Bjarnason, R. Functional Programming in Scala. Manning Publications, 2014. → Ch. 4: “Handling errors without exceptions” → “The Option data type”, pp. 53-60 ↩
-
Chiusano, P. and Bjarnason, R. Functional Programming in Scala. Manning Publications, 2014. → Ch. 12: “Applicative and traversable functors” → “The difference between monads and applicative functors”, pp. 208-210 ↩